Variational Inference

自从接触深度学习后，每每遇到相关数学公式都头疼。其中变分推断出现的频率之多，让我一见它到便跳过直接看与其相关的结果。所以，经常处于模模糊糊半懂不懂的状态，让我十分痛苦。于是，这几天我便想结束这种痛苦，故仔细的看了相关资料，并作如下小结。如若只想简单了解其思想可跳至综述。

变分推断简单来说便是需要根据已有数据推断需要的分布$P$；当$P$不容易表达，不能直接求解时，可以尝试用变分推断的方法。即，寻找容易表达和求解的分布$Q$，当$Q$和$P$的差距很小的时候，$Q$就可以作为$P$的近似分布代替$P$。

数学推导

学过概率论的人一般都会知道贝叶斯公式：$P(z|x)=\frac{P(x,z)}{P(x)} \tag{1.1}$同理，$P(x,z)=P(x|z)P(z) \tag{1.2}$其中$P(z|x)$被称作后验概率，$P(x|z)$被称为似然度，$P(z)$则是先验概率。经过简单的交换可得：$P(x)=\frac{P(x,z)}{P(z|x)} \tag{1.3}$ 假设$P(x)$便是我们所需要的而且不易表达的分布。

对(1.3)式左右两侧取底为$e$的对数,并且右式同除Q(z)(Q(z)作用下面将解释):

$$\begin{align*}\ln P(x)&=\ln P(x,z)-\ln P(z|x) \tag{1.4}\\ &=\ln{\frac{P(x,z)}{Q(z)}}-\ln{\frac{P(z|x)}{Q(z)}}\\ &=\ln{P(x,z)}-\ln{Q(z)}-\ln{\frac{P(z|x)}{Q(z)}}\\ \end{align*}$$

对于式(1.4)两边取期望：

$$\begin{align*} \int_{z}\ln{P(x)}Q(z)dz&=\ln{P(x)}\tag{1.5}\\ &=\underbrace{\int_z{\ln{P(x,z)}Q(z)dz-\int_z\ln{Q(z)}Q(z)dz}}_{L(Q)-Evidence Lower Bound(ELOB)}\underbrace{-\int_z{\ln{\frac{P(z|x)}{Q(z)}Q(z)dz}}}_{KL(Q||P)}\\ \end{align*}$$

计算到此，我们要思考一个问题：何时ELOB达到最大值？这个问题其实很简单，由于KL散度本身大于等于0,所以$\ln{P(x)}$便是ELOB的上界。 我们不是讨论变分推断吗，为什么讨论起$ELOB$了呢？其实上面我们提到了用$Q$去逼近$P$，所以式(1.4)从而引进了$Q(z)$。而衡量两个分布的相似程度的一种标准便是$KL$散度，$KL$的值越小表示两种分布越相似。什么时候最小呢？只要$KL=0$便是最小，这个条件看似说明了一切，但是我们只知道$Q$不知道$P$的分布啊，没法确定两者是否为0，所以$KL=0$便成了一个鸡肋的条件，食之无味，弃之可惜啊。这时候救世主$ELOB$出现了，她的光辉照耀世界～(中二ing，笑)。

式(1.5)分为两部分，既然我们没法确定$KL$散度，我们只好利用$ELOB$($ELOB$可以看做是$Q(z)$的函数——即函数的函数(泛函，本学渣只听说过没有正式学习过))。既然$KL散度$要得到最小，那么就要设法使$ELOB$到达最大。

是时候展示真正的技术了——$EZ$

下面证明$ELOB$的上界：

$$\begin{align*} \ln{P(x)}=&\ln{\int_z{P(x,z)dz}}\\ &=\ln{\int_z{\frac{P(x,z)}{Q(z)}Q(z)dz}}\\ &=\ln{\Bbb{E_{Q(Z)}}[\frac{P(x,z)}{Q(z)}]}\\ (由詹森不等式可得)&\geq{\Bbb{E_{Q(Z)}}[\frac{\ln{P(x,z)}}{Q(z)}]}\\ &=\underbrace{\Bbb{E_{Q(Z)}}[\ln{P(x,z)}]-\Bbb{E_{Q(Z)}}[\ln{Q(z)}]}_{ELOB}\\ \end{align*}$$

以上我们知道了通过使得$ELOB$最大化的这种间接的方式从而使得$KL$散度尽可能的小，那么接下来便是介绍如何使得$ELOB$尽可能的趋近其上界。

假设$Z$={$z_1,\cdots，z_n$},现实生活中大多数$P(z)\neq{P(z_1)P(z_2)\cdots P(z_n)}$，但是我们选择$Q(z)$时可以选我们知道到的，简单的，独立同分布的概率分布(选非独立同分布的我也不拦着)$Q(z)=Q(z_1)Q(z_2) \cdots Q(z_n)$。选好了$Q(z)$,好戏也要开场了。

$$\begin{align*} \because L(Q) &= \int{Q(z) \ln{P(x,z)}dz}-\int{Q(z)\ln{Q(Z)}dz}\\ &= \underbrace{\int{\prod_{i=1}^{n}{Q_i(z_i)}\ln{P(x,z)dz}}}_{Part1}- \underbrace{\int{\prod_{i=1}^{n}{Q_i(z_i)} \sum_{i=1}^{n}\ln{Q_i(z_i)dz}}}_{Part2} \tag{1.6}\\ Part1&= \int_{z_1} \cdots \int_{z_n} \prod_{i=1}^n Q_i(z_i)\ln{P(x,z)}dz_1 \dots dz_n\\ 当i=j时： Part1 &= \int Q_j(z_j)(\int \cdots \int_{z_{i \neq j}} \prod_{i \neq j}^n Q_i(z_i) \ln P(x,z)\prod_{i\neq j}^ndz_i)dz_j\\ &=\int_{z_j}Q_j(z_j)(\int\cdots \int_{z_{i\neq j}}\ln{P(x,z)}\prod_{i\neq j}^nQ_j(z_j)dz_j)\\ &=\int_{z_j}Q_j(z_j)(\Bbb{E}_{i\neq j}[\ln{P(x,z)}])dz_j\\ 同理，可推出Part2:\\ Part2&=\sum_{i=1}^n(\int_{z_i}Q_i(z_i)\ln Q_i(z_i)dz_i)\\ \end{align*}$$

下面证明$Part2$变量为两个时，可得：

$$\int_{x_1}\int_{x_2}[f(x_1)+f(x_2)]P(x_1)P(x_2)dx_1dx_2=\int_{x_1}f(x_1)P(x_1)dx_1+\int_{x_2}f(x_2)P(x_2)dx_2$$

推至N个时，$Part2$得证。当$i=j$时可简写为：

$$\begin{align*} Part2=\int_{z_i}Q_i(z_i)\ln Q_i(z_i)dz_i+const\\ \end{align*}$$

再令：$\ln{\overline{P}j(x,z_j)}=\Bbb{E}{i\neq j}[\ln{P(x,z)}]$可得：

$$L(Q_j)=Part1-Part2=\int_{z_j}Q_j(z_j)\ln{[\frac{\overline{P}_j(x,z_j)}{Q_j(z_j)}]}dz_j+const \to-KL(\Bbb{E}_{i\neq j}[\ln{P(x,z)}]||Q_j(z_j))$$

推导到这，豁然开朗。原来$ELOB$最后也要化为一个$-KL$散度，故最大值为0当且仅当$\ln{Q_i(z_j)=\Bbb{E}_{i\neq j}[\ln{P(x,z)}]}$。最后，简单说明如何获得稳定$\ln{Q}$的迭代过程：

$$\begin{align*} \ln Q_1^*(z_1)&=\int_{Q_2}\cdots \int_{Q_n}\ln{P(x,z)}Q_2(z_2)\cdots Q_n(z_n)dz_2\cdots dz_n\\ \ln Q_2^*(z_2)&=\int_{Q_1}\cdots \int_{Q_n}\ln{P(x,z)}Q_1^*(z_1)\cdots Q_n(z_n)dz_1\cdots dz_n\\ \vdots\\ \ln Q_n^*(z_n)&=\int_{Q_1}\cdots \int_{Q_{n-1}}\ln{P(x,z)}Q_1^*(z_1)\cdots Q_{n-1}^*(z_{n-1})dz_1\cdots dz_{n-1}\\ \end{align*}$$

经过多次算法迭代，$\ln{Q}$收敛于固定值，从而得到最大$ELOB$，进而确定所需$KL$散度与$Q$分布。

综述

变分推断是利用已知分布通过调整使其符合我们需要却难以用公式表达的分布。由$ELOB$和$KL$散度的关系，通过得到$ELOB$的上界间接获$KL(Q(z)||P(z|x))$散度。对于$ELOB$的上界，又可以通过转化为相关的$KL(\Bbb{E}_{i\neq j}[\ln{P(x,z)}]||Q_j(z_j))$散度求解。当$Q$和$P$的差距很小的时候，$Q$就可以作为$P$的近似分布代替$P$

$$\begin{align*} KL(\Bbb{E}_{i\neq j}[\ln{P(x,z)}]||Q_j(z_j))\to ELOB\to KL(Q(z)||P(z|x)) \to 调整后的Q(z) \end{align*}$$

用一张图来表示$Q$分布的变化。

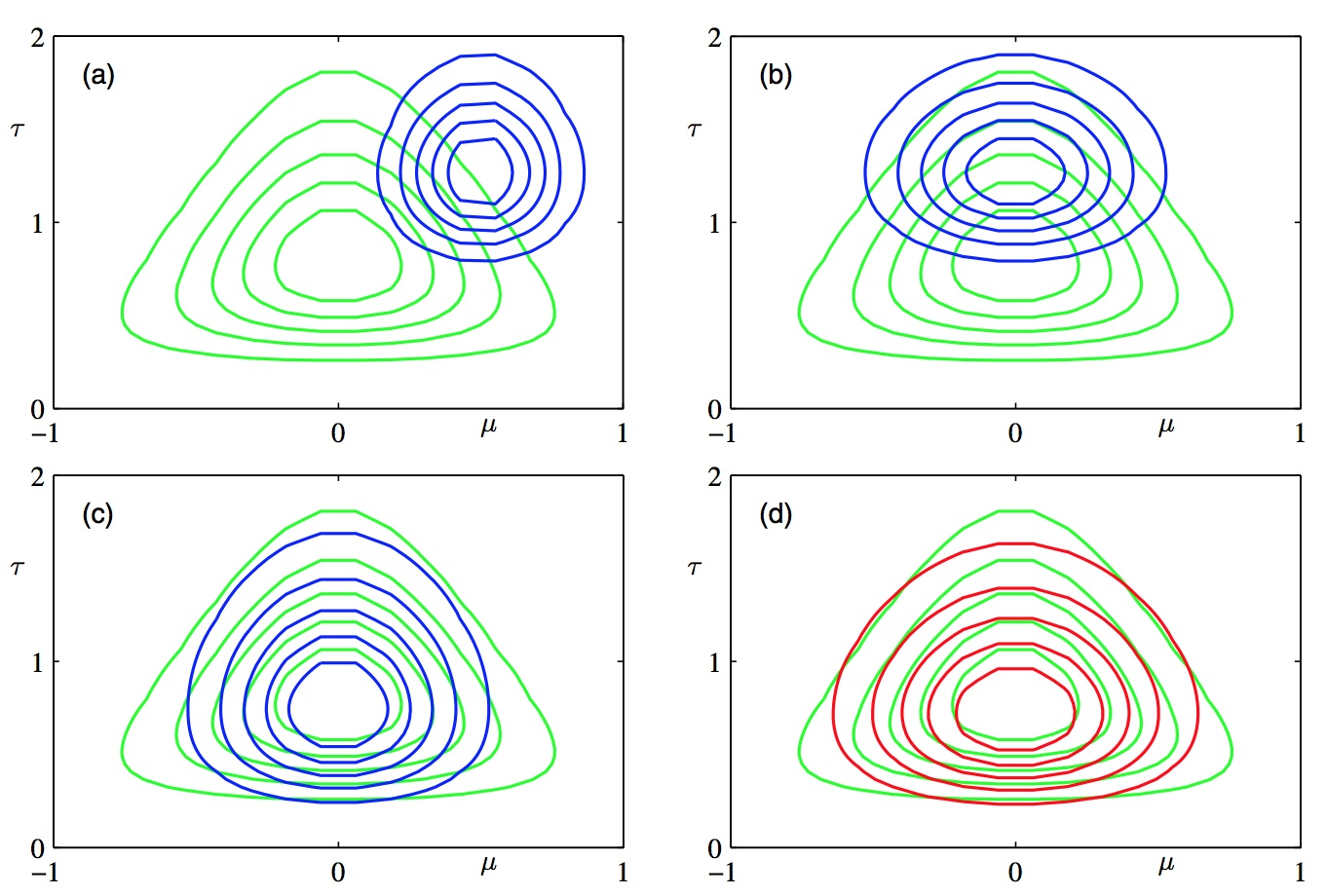
文中配图来源于《徐亦达机器学习》

鄙人不才，不求甚解。

能力有限，才疏学浅。

漏洞百出，不吝赐教。

如若转载，D J 出品。

---

• Next
  Tips